Understanding Markov Chains

Gabriel Egan
De Montfort University, UK

In this undergraduate assignment, students use a manually applied algorithm to generate a Markov Chain from a given short extract of language. Included here are precise instructions with diagrams for two activities where students develop structures to generate text based on probabilities. Through these game-like activities, students discover that Markov Chains efficiently embody the writer's preference for following one particular word with another, which lays the foundation for discussion of how probabilistic language-generation models work. The assignment gives students a concrete way to explore and visualise the building blocks of various language models and understand their implications for linguistics. Any students able to distinguish the essential parts-of-speech such as verb, noun, article, adjective, and relative pronoun should be able to complete the assignment with proper support. (All students able to speak English will already have learnt the meaning of these terms at some point, but a short refresher might be wanted to bring everyone up to the same speed in identifying examples of them in practice.) The assignment has been used to help Creative Writing students understand how Artificial Intelligence is able to produce writing that sounds like it came from a human. In the ‘Follow Up’ section suggestions are given for how more specialist linguistic teaching can be built on this basis, including an exploration of the competing theories for how humans generate new sentences.

Learning Goals:

Better student understanding of the specific means by which a Markov Chain can embody the choices made in human writing
General appreciation of the means by which language preferences can be modelled mathematically

Original Assignment Context: Early stage of an arts and humanities course

Materials Needed: Writing samples (given below)

Time Frame: ~1 week

Introduction

In the 1950s, Noam Chomsky influentially proved that finite-state automata with probabilistically weighted edges -- that is, Markov Chains -- cannot be the fundamental system (or "grammar") for language generation in the human brain, and that something rather more sophisticated, something as powerful as his Transformational Generative Grammar, is needed to account for the rich variety and complexity of language. Chomsky maintained his claim that "a finite state Markov process" could not generate all possible English sentences without also generating "many non-sentences as well" (Chomsky 1957, 24) from his original statement in 1957 until recently, consistently rejecting the proposition that a language model based solely on statistical analysis of large amounts of text could generate new sentences that might pass as actual human expression (Norvig 2017). For Chomsky, a probabilistic word-by-word approach to language generation -- asking at each step "what word is most likely to come next?" -- is fundamentally inadequate to the task. Yet everywhere we now see probabilistic approaches to language generation producing impressive results, particularly those using the newly developed machine-language transformers such as the Generative Pre-Trained Transformer (GPT) from the group OpenAI (Brown et al. 2020).

For undergraduate students to begin to understand these debates about the nature of language and creativity, some practical experience of how Markov Chains model language is helpful. The assignment presented here was created for Arts and Humanities students with little technical knowledge of either computation or linguistics. The students are given a step-by-step guide, a manually applied algorithm, for generating a Markov Chain from a given short extract of language. The tutor chooses the extracts for their effective rhetorical use of repetition so that the resulting Chains contain loops in which nodes are revisited multiple times in different sequences. The resulting student-created Markov Chains lead to discussion of how we can capture aspects of writers' style, such as the preference for following one particular word with another, in such a Chain. This lays the foundation for discussion of how probabilistic language-generation models work.

The intended learning outcome is better student understanding of the specific means by which a Markov Chain can embody the choices made in human writing, as part of a more general appreciation of the means by which language preferences can be modelled mathematically. The tutor may preselect her own writing samples or start with the ones shown here. There are no special prerequisites for students or tutors, and suitable pre-class preparation would be a couple of online tutorial videos (of the kind widely available on YouTube) about Markov Chains. This assignment has been used in the academic year 2022-2023 as the main exercise of one two-hour practical workshop on the year-long final-year BA English course called "Artificial Intelligence and Creative Writing" taught at De Montfort University in Leicester, England.

Previous Learning

In earlier classes in this course, the students experimented with a Recursive Transition Network of the kind depicted on page 132 of Douglas Hofstadter's book Godel, Escher Bach (Hofstadter 1980), reproduced here as Figure One. For each type of word in Hofstadter's picture (article, adjective, noun, and so on) the students were given a stack of index cards, with one word of that type written on each card.

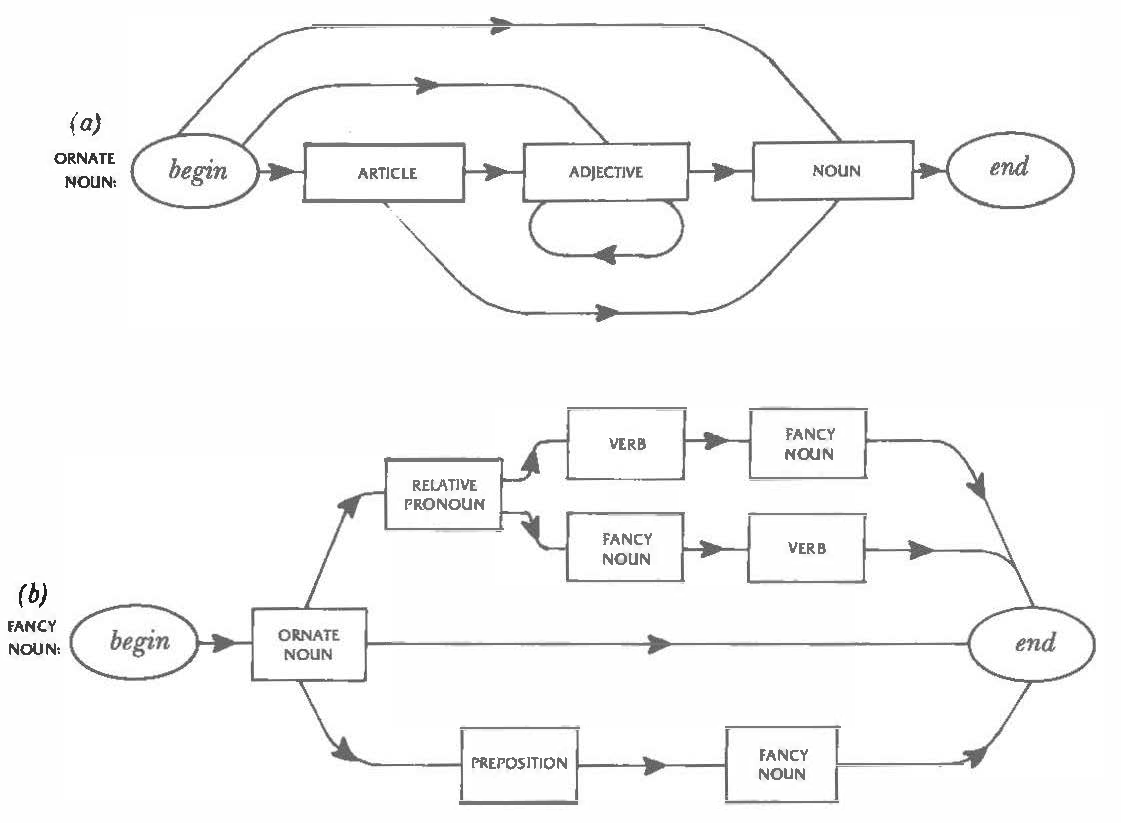
Figure 1. Figure 27 from Douglas Hofstadter's book Gödel, Escher, Bach, p. 132

Using a large printout of Figure One, the students first wrote a probability on each outgoing arrow, known as an edge, that leaves each box, known as a node. The idea is that the probabilities govern the path we take when traversing the network from the node labelled "begin" to the node labelled "end". There is only one edge coming out of "PREPOSITION" in Figure One, so the probability of taking that edge as we leave "PREPOSITION" is certainty (also called unity or simply the value "1"). But there are three edges coming out of "ORNATE NOUN" so the students label each edge with a probability represented as the result of a throw of a single six-sided die. No thought is put into the numbers chosen so long as the probabilities for all the edges leaving the node add up to one. Thus the students might label the edge from "ORNATE NOUN" to "RELATIVE PRONOUN" as "1" (giving a 1/6 chance of following that edge), the edge from "ORNATE NOUN" to "end" as "2 or 3 or 4" (giving a 3/6 or in other words a 1/2 chance of following that edge), and label the edge from "ORNATE NOUN" to "PREPOSITION" as "5 or 6" (for a 2/3 or 1/3 chance of following that edge).

With all the edges labelled, students placed a marker (a small figurine) on the "begin" node in the top half, section (a), of Figure One and repeatedly rolled a die to move from node to node along the weighted edges. As they landed on each node they took one index card from the heap for that node (so first of all a card for either "NOUN", "ADJECTIVE", or "ARTICLE") and placed it on the desk as the next word in a growing phrase that this process constructs. A key concept that working with Figure One helps to convey is that of recursion, since the definition of "FANCY NOUN" in section (b) is a series of nodes including two that are also called "FANCY NOUN". That is, the definition of "FANCY NOUN" is self-reflexive. When traversing the network to produce a "FANCY NOUN", the students occasionally landed on this internal node "FANCY NOUN and had to suspend their current traversal (recording where they had got to) and reenter the "FANCY NOUN" network at the "begin" node. When this inner traversal was completed by landing on "end", the students returned to the outer traversal by picking up where they left off.

To see recursion in practice, consider the die dictating the following traversal of a sequence of nodes, producing their associated words:

(b) "FANCY NOUN"
start at "begin"
landing on "ORNATE NOUN" causes jump to section (a)
    start at "begin"
    landing on "ARTICLE" yields "the"
    landing on "ADJECTIVE" yields "red"
    landing on "NOUN" yields "balloon"
    landing on "end" causes return to section (b) at node "ORNATE NOUN"
landing on "RELATIVE PRONOUN" yields "that"
landing on "FANCY NOUN" causes reentrant jump back into section (b)
    start at "begin"
    landing on "ORNATE NOUN" causes jump to section (a)
        start at "begin"
        landing on "ARTICLE" yields "the"
        landing on "NOUN" yields "baker"
        landing on "end" causes return to section (b) at node "ORNATE NOUN"
    landing on "PREPOSITION" yields "in"
    landing on "FANCY NOUN" causes reentrant jump back into section (b)
        start at "begin"
        landing on "ORNATE NOUN" yields jump to section (a)
            start at "begin"
            landing on "ARTICLE" yields "a"
            landing on "ADJECTIVE" yields "strong"
            landing on "NOUN" yields "station"
            landing on "end" causes return to section (b) at node "FANCY
NOUN" in lower path
        landing on "end" causes return to section (b) at node "FANCY NOUN"
in upper path
landing on "VERB" yields "receives"
landing on "end" causes termination of traversal

The resulting fancy noun yielded by this hypothetical traversal of the Recursive Transition Network (reading the above "yields" items in order) is "the red balloon that the baker in a strong station receives", which is indeed fancy. The process of recursion, which Chomsky identified as a key element of human generation of language, is here marked by the "reentrant jumps" by which the steps for producing a "FANCY NOUN" themselves invoke the steps for producing a "FANCY NOUN". Such self-reference is allowable in a step-by-step algorithm so long as there is at least one path through the network that avoids the self-reference. In Figure One, the central pathway for "FANCY NOUN" is from "begin" to "ORNATE NOUN" to "end", avoiding the self-references of the upper and lower paths. By eventually taking this central path the process bottoms out and avoids infinitely extended self-reference. It is theoretically possible for the process to generate an infinitely long phrase by always avoiding this central path, and with certain choices of weights the process will in practice produce inordinately long (but always grammatically correct) ones.

In multiple runs of this exercise, students were allowed to vary their choices of weightings and observe how these affected the phrases generated. Notice that with a jump from section (b) to section (a), or a reentrant jump from section (b) into itself, we have to keep track of where we came from before we made the jump so that we can return to that place when we land on the "end" node in the section jumped to. And since a reentrant jump can itself initiate a further reentrant jump, we might end up managing a stack of such reminders of where to return to. In computer science the data structure used for this purpose is actually called a stack, and in Chomsky's Transformational Generative Grammar keeping this stack of suspended operations in the brain's short-term memory is one of the reasons that complicated (and, in particular, ill-constructed) sentences are cognitively taxing to parse.

The weeks following the exercise with Figure One included tasks for watching videos scraped from online sources (particularly YouTube) on the topics of finite-state automata and Markov Chains, and extracts from books that explain Chomsky's work including John Lyons's Chomsky (Lyons 1970) and Steven Pinker's The Language Instinct (Pinker 1995). This prepared students for the task of the present assignment, which is to progress from simply following a network of the kind shown in Figure One to creating such a network for themselves using a given piece of writing as its basis.

The Assignment

The network shown in Figure One became a Markov Chain once the students added the probability weightings to its edges. Doing this provided for each node (containing the name of a word type) a probability distribution shaping the outcome of the randomized selection of which word will come next in a growing sequence. Figure One was devised with an understanding of English grammar applied to the choices of labels in the nodes (the word types) so that traversing this network would inevitably produce phrases of good English (in the sense that follows grammatical rules). What if we could create such a Markov Chain from existing writing and without a knowledge of the rules of English phrase and sentence construction? The manual exercise of creating such a Chain mirrors what happens when an Artificial Intelligence is trained on existing bodies of writing rather than being programmed with the underlying rules of language: the rules become embodied in the nodes and weighted edge of the Markov Chain.

The present assignment consists of a simple algorithm for students to follow using sample texts chosen by the tutor. The sample texts should be between 10 and 50 words in length if the task is to be completed in class time, should contain as many repetitions of words as possible, and should have all their punctuation removed. Repetition within the text is essential. The Markov Chain derived from the sentence "Now is the winter of our discontent" is uninteresting because there will be as many nodes as word tokens (precisely seven) and the Chain will be a single line of arrows from "Now" to "discontent". The Markov Chain for "it was the best of times it was the worst of times" (Figure Two), on the other hand, is interesting because of the choice between "best" and "worst" after "it was the" and because after "times" the sentence might either end or return to "it".

This is the algorithm given to the students for making the Markov Chain from a given text:

Draw a "[Start"] box on the left side of your piece of paper and to the right of it draw a box containing the first word of the text. Draw an arrow linking "[Start]" to the first word of the text. Think of that first word as the "Current word" and underline it in the text to keep track of where you are.
If the underlined "Current word" is the last word in the text and it already has an arrow to a "[Stop]" box, stop the assignment. If the underlined "Current word" is the last word in the text and it does not already have an arrow to a "[Stop]" box, draw a "[Stop]" box to the right of the box for "Current word" and link the "Current word" box to the [Stop] box with an arrow and then stop this assignment.
If the underlined "Current word" is not the last word in the text, count how many times "Current word" appears in the text (including the underlined occurrence) and write that number down underneath a forward-slash division sign, as in "/3" if "Current word" appears in the text three times.
On a spare piece of paper, make a "Comes next" list for "Current word" as follows. For each occurrence of "Current word" in the text, including the underlined one, write down the single word that immediately follows it. Beside each of these words that "Comes next" write how many times it "Comes next" after the "Current word" in the text and follow that count with the divisor from Step (3). Thus, if "Current word" appears in the text three times there must be three words that follow "Current word", but they are not necessarily three different words. If "Current word" is followed by the word "the" two times and is followed by the word "on" one time, write down "the 2/3" and "on 1/3" in the "Comes next" list. If one of the occurrences of "Current word" in the text is the last word in the text, add the item "[Stop]" to the "Comes next" list and add its fraction (which will be 1 over the number of occurrences of "Current word" in the text).
Returning to your Markov Chain, draw a box to the right of the "Current word" box for each of the words (or the "[Stop]" token) in the "Comes next" list you made in Step (4) that you don't already have a box for, then put the word (or the "[Stop]" token) from the "Comes next" list inside the box and draw an arrow from the "Current word" box to each of these new boxes. If one of the words (or the "[Stop]" token) in the "Comes next" list made in Step (4) already has a box drawn in a previous step, don't draw a new box but instead draw the arrow from the "Current word" box to the existing box. Beside each arrow put the associated "weight" from the "Comes next" list made in Step (4). Thus, if "Current word" is followed by the word "the" two times and is followed by the word "on" one time, write beside the arrow from the "Current word" box to the "the" box the fraction "2/3" and write beside the arrow from the "Current word" box to the "on" box the fraction "1/3".
Cross "Current word" off from the text. The next word in the text is your new "Current word", so underline it. You must already have a box for this new "Current word" since you just drew it in Step (5) or in a previous iteration of that step.
Go to Step 2.

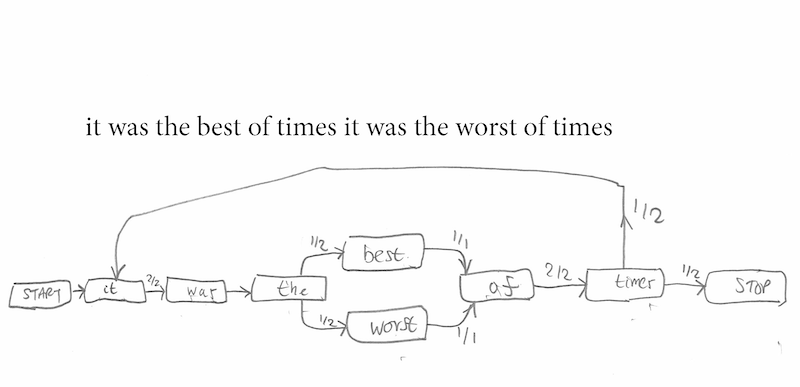
Figure 2. A simple Markov Chain from a simple text with little repetition.

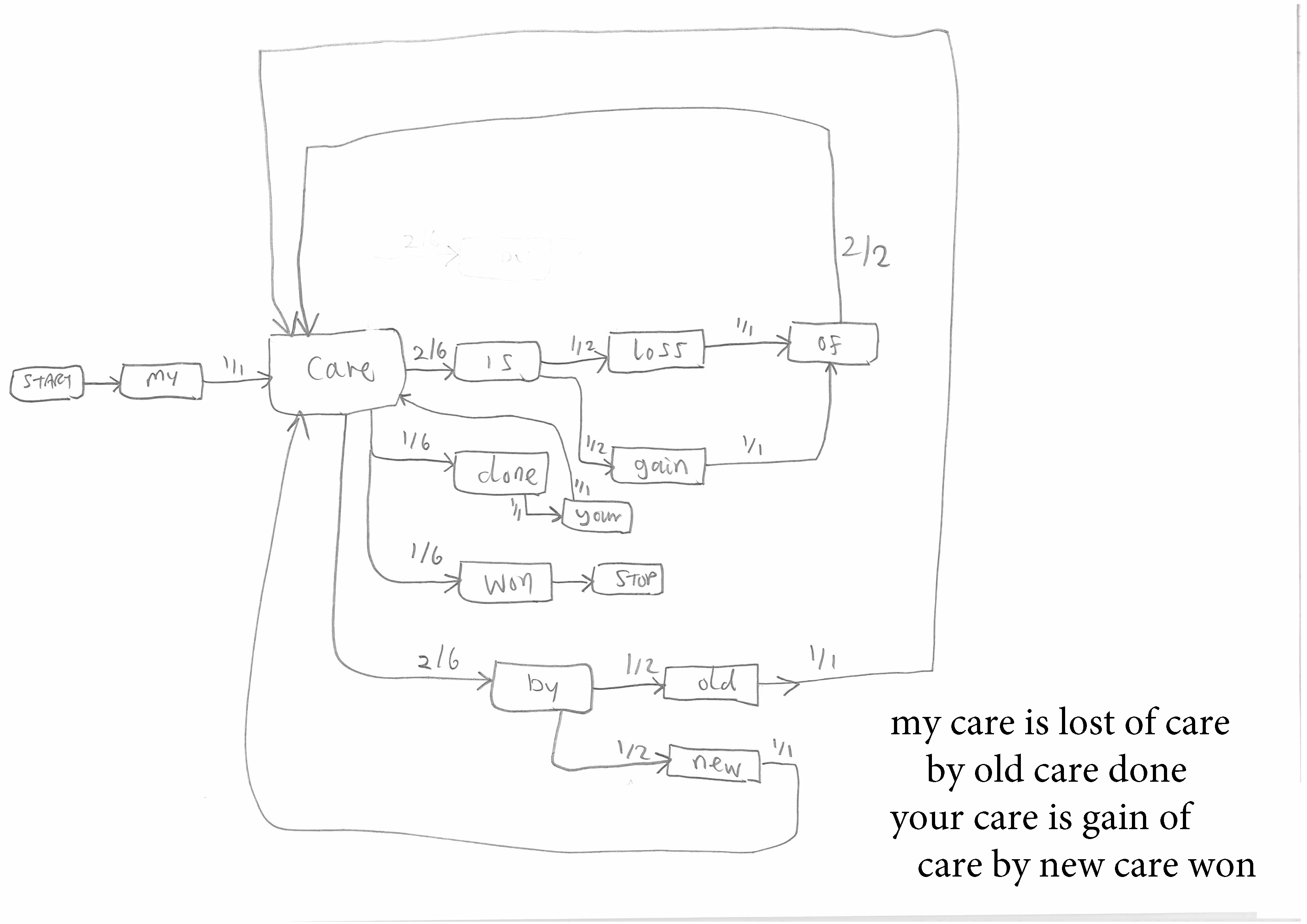
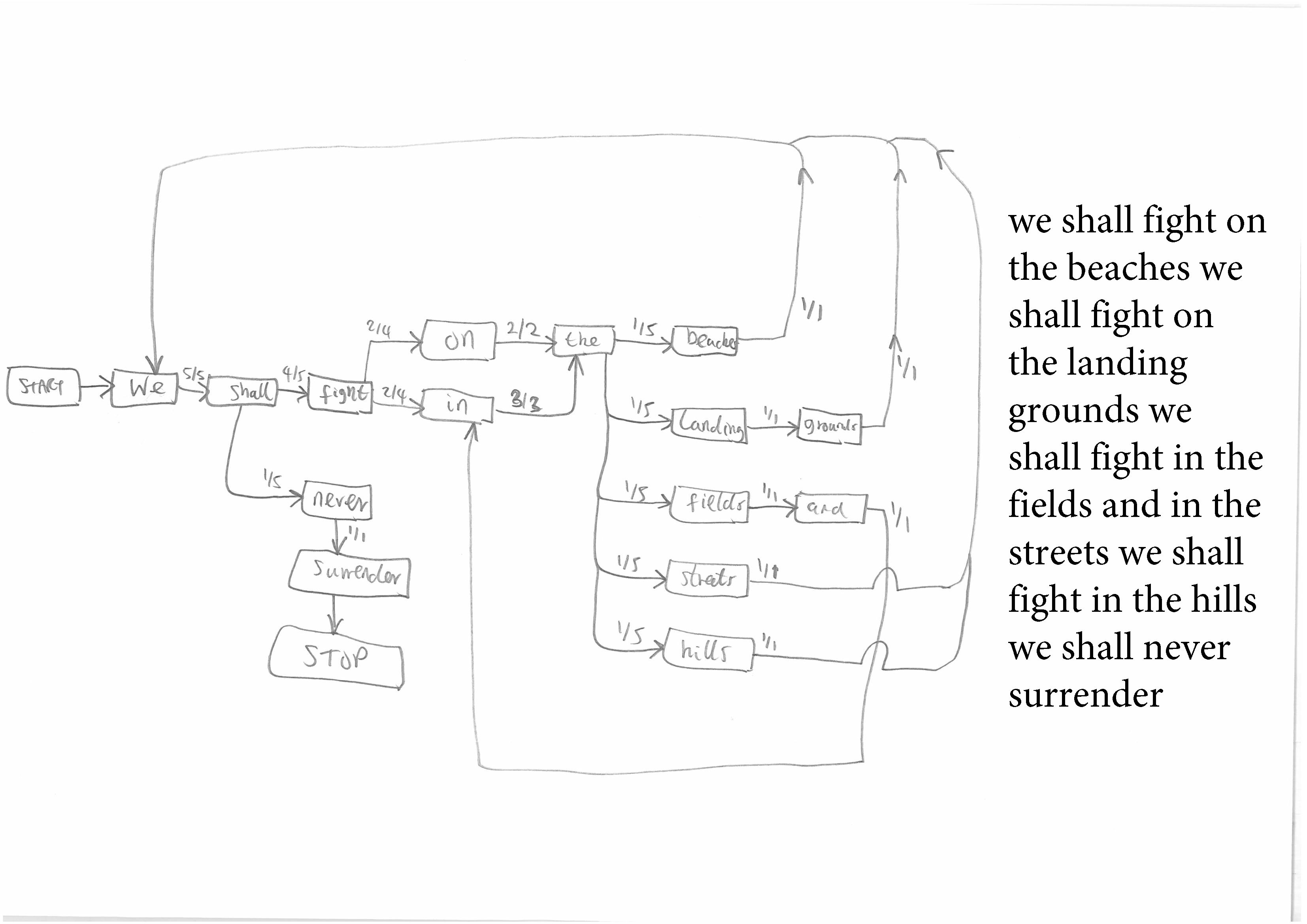Figure 3 and 4. More complex Markov Chains from longer and more repetitive texts.

This assignment should be completed for short repetitive texts that give simple but interesting Chains of the kind shown in Figure Two before students move on to longer and complex texts that give rise to the complex Chains shown in Figures Three and Four. The author's penchant is for Shakespearian sentences such as "fair is foul and foul is fair", but any short sentence with repetition is suitable.

Once the students have grasped the making of a few such Markov Chains, the Chains can be used to generate new text by traversing the network using the weight on each edge as the probability of following that edge. For this purpose some random numbers are needed. The author finds it easiest to convert the weights on the arrows to the results from rolls of a die, so that a probability of "1/3" becomes "a roll of 1 or 2" (that is, two of the six possible numbers on a die, hence a probability of one-in-three). The rolling of a die in class has attractive tactile and kinaesthetic aspects. (Pro-tip: use a 'captive' die inside a transparent box to save repeated scrabbling on the floor to recover lost dice.) Alternatively, a computer-based random-number generator will work just as well.

If the Markov Chains have been created properly, every traversal ought to produce sentences that are grammatically acceptable, or that could be made so by inserting their missing punctuation. Some Chains may allow an early termination before a main verb has been encountered. For instance, because the text "fair is foul and foul is fair" starts and ends with the same word, "fair", one possible route through the resulting Markov Chain simply produces the sentence "fair" and then stops. Such cases may be discussed in relation to the fact that a broader range of sentences are permitted in dramatic and cinematic dialogue (that is, as characters' speeches) than may be found in discursive prose. Just why randomized traversals of Markov Chains produce grammatically acceptable sentences, and the extent to which they approach the orderliness of the linguistically originated network in Figure One, are fruitful topics for student discussion.

Follow Up

The above assignment can form the basis of an exploration of the competing theories for how the mind creates language. One possible next step is teaching the technique of tree-diagramming a sentence, popularised by Chomsky in his book Syntactic Structures (Chomsky 1957). After they have tried the assignment described here, it is useful to engage in a wider debate concerning the need for a linguistic basis to any language-generating system. Must we model how language is generated in the human mind in order to create any convincing mechanical language generator (as Chomsky has asserted) or may we rely on statistical modelling of a large body of existing writing (as do the current crop of language models in Artificial Intelligence)? The fact that current Artificial Intelligence models can be prompted into saying things that no human would say might indicate remaining limitations to the statistical approach. In practical follow-up to this assignment, hands-on experiments with the existing Artificial Intelligence models may illustrate these limitations.

The engineering and computational aspects of this topic cannot be taken much further in an undergraduate course for Humanities students. But one fruitful line of further enquiry that arises from the above is the use of Context Free Grammars to generate writing. As part of their introduction to tree-diagramming, students in this course are taught Chomskyan "production rules" of the kind "S -> NP + VP", which means "A Sentence can be expanded into a Noun Phrase and a Verb Phrase", and "NP -> NP + that + VP", which means "A Noun Phrase can be expanded into a Noun Phrase follow by the word 'that' followed by a Verb Phrase". In this topic too we can move from the creation of a model that encapsulates what is done in given sentences to the reuse of the model for the generation of new sentences. For this the Context Free Grammar systems RiTA and Tracery described elsewhere in this volume are especially helpful.

Acknowledgments

De Montfort University doctoral candidate Mr Nathan Dooner, who is researching the use of machine-learning techniques to determine authorship in disputed cases, assisted in the creation and the classroom delivery of the material described here. De Montfort University's Professor of Creative Writing, Simon Perril, created and delivers complementary teaching materials that explore pre-computational approaches to the mechanization of language generation.

License

The present work is hereby offered without restriction for all uses, including commercial ones, under a Creative Commons Attribution 2.0 Generic (CC BY 2.0) license.

Works Cited

Brown, Tom B., Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel M. Ziegler, Jeffrey Wu, Clemens Winter, Christopher Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever and Dario Amodei. 2020. "Language Models Are Few-Shot Learners [Introducing GPT-3]." arXiv 2005.14165. 1-75.

Chomsky, Noam. 1957. Syntactic Structures. Janua Linguarum Series Minor. 4. The Hague. Mouton.

Hofstadter, Douglas R. 1980. Gödel, Escher, Bach: An Eternal Golden Braid. Harmondsworth. Penguin.

Lyons, John. 1970. Chomsky. Modern Masters. London. Collins.

Norvig, Peter. 2017. "On Chomsky and the Two Cultures of Statistical Learning." Berechenbarkeit Der Welt?: Philosophie und Wissenschaft im Zeitalter Von Big Data [Predictability of the World?: Philosophy and Science in the Age of Big Data]. Edited by Wolfgang Pietsch, Jörg Wernecke and Maximilian Ott. Wiesbaden. Springer. 61-83.

Pinker, Steven. 1995. The Language Instinct: The New Science of Language and Mind. London. Penguin.