
This fold is a common first fold to be taught. The model serves the utilitarian purpose of being a container for other models. Magazine covers serve well here. The model requires a rectangle. This is, in fact, a good question to ask students.
The three diagrams were made using Visual Basic. This was useful for making
dotted lines and also exact measurements. The images were 'captured' into Paint
Shop Pro. The folding in of the corners proved easier to do in Paint Shop Pro
using the zoom feature and erasing lines by writing with the background color.
The procedure for making the box is:
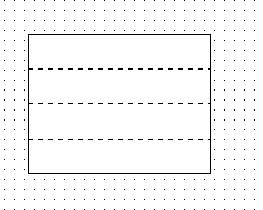
| 1. Fold the paper in half along the long dimension. Unfold. Fold the edges to the centerline. Unfold. |
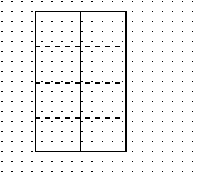
| 2. Repeat in the other direction: fold in half, short side to short
side. Unfold. Fold sides to centerline. You can ask about the symmetries in the model. |
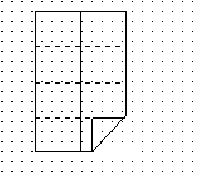
| 3. There are three fold lines perpendicular to each folded edge. Fold a corner up to the nearest line. |
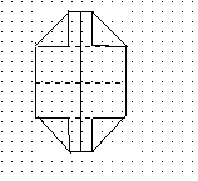
| 4. Repeat with remaining corners. |
| 5. Fold inner raw edges out over corners to lock model. |
Why does this work? The answer is first of all, that the sides not being equal gives rise to the potential flap. The flap locks the corners. The locked corners mean the sides of the box stay together.
What are the final dimensions: sides of the base and the height of the box? Also, what is the size of the flaps? Consider framing this question in terms of the abstract L for long and S for short sides. This use of the algebraic paradigm arises quite naturally so take advantage! The following is a series of probing questions:
Let's go back in the folding procedure to when the short sides are folded into the center. You have two columns of 4 little rectangles. What are the dimensions of each rectangle? Is it similar to the original rectangle? The dimensions are ¼ of L by ¼ of S so, therefore, it is similar.
So now fold up the corners. The folded corner does not cover the whole rectangle. Why not? Because L is bigger than S. What is the linear measurement of the leftover amount? It is ¼ times (L - S).
Now we can calculate the dimensions of the model. The height is the side of the corners, which is ¼ of S. For the dimensions of the base of the box, look at it! The first folds divide the paper into 4 parts-What is a good term for these? You may get a spontaneous response that the long strips have thickness ¼ of S and length L and the ones going the other way, the short ones, have thickness ¼ of L and length S. The final box has a base two of the long ones by two of the short ones. So the base is ½ times S by ½ times L.
Now, measure the actual dimensions of the original paper. Substitute (or to use a more familiar phrase, stick in) the values. Then measure the model. Is it exactly the same? How exact? What are sources for any discrepancies?